I. บทนำ
น้ำสามารถจุดเทียนได้จริงหรือ?มันเป็นความจริง!
จริงหรือที่งูกลัวหลัวการ์?มันเป็นเท็จ!
สิ่งที่เราจะพูดคุยในวันนี้คือ:
การรบกวนสามารถปรับปรุงความแม่นยำในการวัดได้ จริงหรือไม่?
ภายใต้สถานการณ์ปกติ การรบกวนถือเป็นศัตรูธรรมชาติของการวัดค่าการรบกวนจะลดความแม่นยำในการวัดในกรณีที่รุนแรง การวัดจะไม่ดำเนินการตามปกติจากมุมมองนี้ การรบกวนสามารถปรับปรุงความแม่นยำในการวัดได้ ซึ่งถือว่าผิด!
อย่างไรก็ตาม เป็นเช่นนี้เสมอหรือไม่?มีสถานการณ์ที่การรบกวนไม่ทำให้ความแม่นยำในการวัดลดลง แต่ปรับปรุงให้ดีขึ้นแทนหรือไม่
คำตอบคือใช่!
2. ข้อตกลงการแทรกแซง
เมื่อรวมกับสถานการณ์จริงแล้ว เราทำข้อตกลงต่อไปนี้เกี่ยวกับการแทรกแซง:
- การรบกวนไม่มีส่วนประกอบ DCในการวัดจริง สัญญาณรบกวนส่วนใหญ่เป็นสัญญาณรบกวน AC และสมมติฐานนี้สมเหตุสมผล
- เมื่อเทียบกับแรงดันไฟฟ้ากระแสตรงที่วัดได้ ความกว้างของการรบกวนจะค่อนข้างเล็กซึ่งสอดคล้องกับสถานการณ์จริง
- การรบกวนเป็นสัญญาณเป็นระยะ หรือค่าเฉลี่ยเป็นศูนย์ภายในระยะเวลาที่กำหนดประเด็นนี้ไม่จำเป็นต้องเป็นจริงในการวัดจริงอย่างไรก็ตาม เนื่องจากสัญญาณรบกวนโดยทั่วไปเป็นสัญญาณ AC ความถี่ที่สูงกว่า สำหรับการรบกวนส่วนใหญ่ การใช้ค่าเฉลี่ยเป็นศูนย์จึงมีความสมเหตุสมผลในระยะเวลาที่นานขึ้น
3. ความแม่นยำในการวัดภายใต้การรบกวน
ปัจจุบันเครื่องมือวัดและมิเตอร์ไฟฟ้าส่วนใหญ่ใช้ตัวแปลง AD และความแม่นยำในการวัดมีความสัมพันธ์อย่างใกล้ชิดกับความละเอียดของตัวแปลง ADโดยทั่วไปแล้ว ตัวแปลง AD ที่มีความละเอียดสูงกว่าจะมีความแม่นยำในการวัดสูงกว่า
อย่างไรก็ตาม ความละเอียดของ AD นั้นมีจำกัดอยู่เสมอสมมติว่าความละเอียดของ AD คือ 3 บิตและแรงดันไฟฟ้าในการวัดสูงสุดคือ 8V ตัวแปลง AD จะเทียบเท่ากับสเกลที่แบ่งออกเป็น 8 ส่วน แต่ละส่วนคือ 1Vคือ 1Vผลการวัดของ AD นี้จะเป็นจำนวนเต็มเสมอ และส่วนทศนิยมจะถูกยกไปหรือทิ้งไปเสมอ ซึ่งถือว่าต้องมีในบทความนี้การถือหรือการทิ้งจะทำให้เกิดข้อผิดพลาดในการวัดตัวอย่างเช่น 6.3V มากกว่า 6V และน้อยกว่า 7Vผลการวัด AD คือ 7V และมีข้อผิดพลาด 0.7Vเราเรียกข้อผิดพลาดนี้ว่าข้อผิดพลาดในการวัดปริมาณ AD
เพื่อความสะดวกในการวิเคราะห์ เราถือว่าสเกล (ตัวแปลง AD) ไม่มีข้อผิดพลาดในการวัดอื่นๆ ยกเว้นข้อผิดพลาดในการวัดปริมาณ AD
ตอนนี้เราใช้สเกลที่เหมือนกันทั้งสองเพื่อวัดแรงดันไฟฟ้ากระแสตรงสองตัวที่แสดงในรูปที่ 1 โดยไม่มีการรบกวน (สถานการณ์ในอุดมคติ) และด้วยการรบกวน
ดังแสดงในรูปที่ 1 แรงดันไฟฟ้ากระแสตรงที่วัดได้จริงคือ 6.3V และแรงดันไฟฟ้ากระแสตรงในรูปด้านซ้ายไม่มีการรบกวนใด ๆ และเป็นค่าคงที่รูปทางด้านขวาแสดงกระแสตรงที่ถูกรบกวนโดยกระแสสลับ และมีความผันผวนของค่าอยู่บ้างแรงดันไฟฟ้ากระแสตรงในแผนภาพด้านขวาจะเท่ากับแรงดันไฟฟ้ากระแสตรงในแผนภาพด้านซ้ายหลังจากกำจัดสัญญาณรบกวนแล้วสี่เหลี่ยมสีแดงในรูปแสดงถึงผลลัพธ์การแปลงของตัวแปลง AD
แรงดันไฟฟ้า DC ในอุดมคติโดยไม่มีการรบกวน
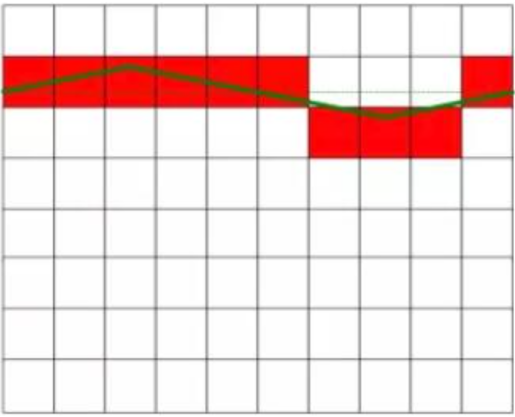
ใช้แรงดันไฟฟ้ากระแสตรงรบกวนด้วยค่าเฉลี่ยเป็นศูนย์
ทำการวัดกระแสตรง 10 ครั้งในสองกรณีตามรูปด้านบน จากนั้นจึงหาค่าเฉลี่ยของการวัด 10 ครั้ง
สเกลแรกทางด้านซ้ายวัด 10 ครั้ง และค่าที่อ่านได้จะเท่ากันในแต่ละครั้งเนื่องจากอิทธิพลของข้อผิดพลาดในการวัดปริมาณ AD การอ่านแต่ละครั้งคือ 7Vหลังจากเฉลี่ยการวัด 10 ครั้ง ผลลัพธ์ยังคงเป็น 7Vข้อผิดพลาดในการวัดปริมาณโฆษณาคือ 0.7V และข้อผิดพลาดในการวัดคือ 0.7V
ระดับที่สองทางด้านขวามีการเปลี่ยนแปลงอย่างมาก:
เนื่องจากความแตกต่างในด้านบวกและลบของแรงดันไฟฟ้ารบกวนและแอมพลิจูด ข้อผิดพลาดในการวัดปริมาณ AD จึงแตกต่างกันที่จุดการวัดที่ต่างกันภายใต้การเปลี่ยนแปลงของข้อผิดพลาดในการวัดปริมาณ AD ผลลัพธ์การวัด AD จะเปลี่ยนระหว่าง 6V ถึง 7Vการวัดเจ็ดครั้งคือ 7V มีเพียงสามการวัดเท่านั้นคือ 6V และค่าเฉลี่ยของการวัด 10 ครั้งคือ 6.3V!ข้อผิดพลาดคือ 0V!
ในความเป็นจริง ไม่มีข้อผิดพลาดที่เป็นไปไม่ได้ เพราะในโลกวัตถุประสงค์ ไม่มี 6.3V ที่เข้มงวด!อย่างไรก็ตาม มีจริง:
ในกรณีที่ไม่มีการรบกวน เนื่องจากผลการวัดแต่ละครั้งจะเหมือนกัน หลังจากเฉลี่ยการวัด 10 ครั้ง ข้อผิดพลาดยังคงไม่เปลี่ยนแปลง!
เมื่อมีการรบกวนในปริมาณที่เหมาะสม หลังจากเฉลี่ยการวัด 10 ครั้ง ข้อผิดพลาดในการวัดปริมาณ AD จะลดลงตามลำดับความสำคัญ!ความละเอียดได้รับการปรับปรุงตามลำดับความสำคัญ!ความแม่นยำในการวัดยังได้รับการปรับปรุงตามลำดับความสำคัญ!
คำถามสำคัญคือ:
จะเหมือนกันหรือไม่เมื่อแรงดันไฟฟ้าที่วัดได้เป็นค่าอื่น?
ผู้อ่านอาจต้องการปฏิบัติตามข้อตกลงเกี่ยวกับการรบกวนในส่วนที่สอง แสดงการรบกวนด้วยชุดค่าตัวเลข ซ้อนการรบกวนบนแรงดันไฟฟ้าที่วัดได้ จากนั้นคำนวณผลการวัดของแต่ละจุดตามหลักการดำเนินการของตัวแปลง AD จากนั้นคำนวณค่าเฉลี่ยสำหรับการตรวจสอบ ตราบใดที่แอมพลิจูดของสัญญาณรบกวนอาจทำให้การอ่านค่าหลังจากการหาปริมาณ AD เปลี่ยนแปลง และความถี่ในการสุ่มตัวอย่างสูงเพียงพอ (การเปลี่ยนแปลงของแอมพลิจูดของสัญญาณรบกวนมีกระบวนการเปลี่ยนผ่าน แทนที่จะเป็นค่าบวกและลบสองค่า ) และต้องปรับปรุงความแม่นยำ!
สามารถพิสูจน์ได้ว่าตราบใดที่แรงดันไฟฟ้าที่วัดไม่ได้เป็นจำนวนเต็ม (ไม่มีอยู่ในโลกวัตถุประสงค์) ก็จะมีข้อผิดพลาดในการวัดปริมาณ AD ไม่ว่าข้อผิดพลาดในการวัดปริมาณ AD จะมีขนาดใหญ่เพียงใด ตราบใดที่แอมพลิจูดของ การรบกวนมากกว่าข้อผิดพลาดเชิงปริมาณ AD หรือมากกว่าความละเอียดขั้นต่ำของ AD จะทำให้ผลการวัดเปลี่ยนแปลงระหว่างค่าสองค่าที่อยู่ติดกันเนื่องจากการรบกวนมีความสมมาตรทั้งเชิงบวกและเชิงลบ ขนาดและความน่าจะเป็นของการลดลงและการเพิ่มขึ้นจะเท่ากันดังนั้น เมื่อค่าจริงใกล้กับค่าใด ความน่าจะเป็นที่ค่าใดจะปรากฏจะมีมากกว่า และจะใกล้เคียงกับค่าใดหลังจากการหาค่าเฉลี่ย
นั่นคือ: ค่าเฉลี่ยของการวัดหลายครั้ง (ค่าเฉลี่ยการรบกวนคือศูนย์) จะต้องใกล้กับผลการวัดมากขึ้นโดยไม่มีการรบกวน กล่าวคือ การใช้สัญญาณรบกวน AC ที่มีค่าเฉลี่ยเป็นศูนย์และการเฉลี่ยการวัดหลายครั้งสามารถลด AD Quantize ที่เท่ากันได้ ปรับปรุงความละเอียดในการวัด AD และปรับปรุงความแม่นยำในการวัด!
เวลาโพสต์: Jul-13-2023
